Find two lines, that the container contains the most water

Pratap SharmaMay 17th, 20214 mins read

Problem

Write a function:

function maxArea(height);

that, given n positive integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of the line i is at (i, ai) and (i, 0). Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container.

Examples

Given height = [1,8,6,2,5,4,8,3,7], the function should return 49.

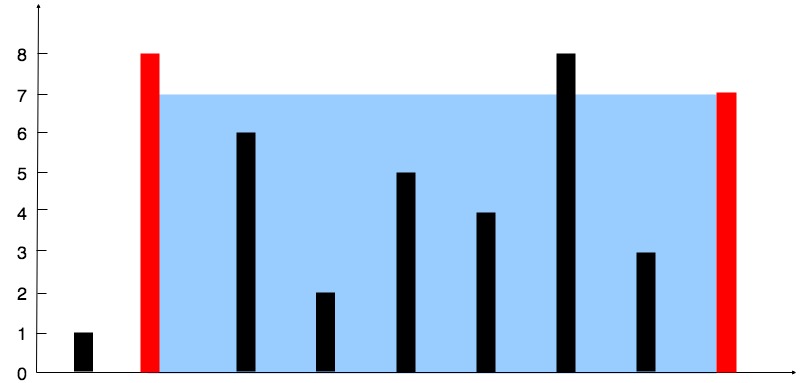
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Given height = [1,1], the function should return 1.
Given height = [4,3,2,1,4], the function should return 16.
Given height = [1,2,1], the function should return 2.

Write an efficient algorithm for the following assumptions

n == height.length
2 <= n <= 105
0 <= height[i] <= 104

You can find the link of the question here.

Solutions

Brute force solution

/**
 * @param {number[]} height
 * @return {number}
 */
function maxArea(height) {
  let maxArea = 0;

  for (let i = 0; i < height.length; i++) {
    for (let j = i + 1; j < height.length; j++) {
      const currArea = Math.min(height[i], height[j]) * (j - i);
      maxArea = Math.max(maxArea, currArea);
    }
  }

  return maxArea;
}

BigO Notation

Time	Space
O(N^2)	O(1)

Optimal Solution

/**
 * @param {number[]} height
 * @return {number}
 */
function maxArea(height) {
  let maxArea = 0;
  let leftPointer = 0;
  let rightPointer = height.length - 1;

  while (leftPointer < rightPointer) {
    const currArea =
      Math.min(height[leftPointer], height[rightPointer]) *
      (rightPointer - leftPointer);
    if (height[leftPointer] < height[rightPointer]) {
      leftPointer++;
    } else {
      rightPointer--;
    }
    maxArea = Math.max(maxArea, currArea);
  }

  return maxArea;
}

BigO Notation

Time	Space
O(N)	O(N)

Solution in Python

class Solution:
    def maxArea(self, height: List[int]) -> int:
        max_area = 0
        left_pointer = 0;
        right_pointer = len(height) - 1

        while left_pointer < right_pointer:
            curr_area = min(height[left_pointer], height[right_pointer]) * (right_pointer - left_pointer)
            max_area = max(curr_area, max_area)
            if height[left_pointer] < height[right_pointer]:
                left_pointer += 1
            else:
                right_pointer -= 1
        return max_area

The solutions above are pretty self-explanatory.

💌 If you’d like to receive more coding solutions in your inbox, you can sign up for the newsletter here.